Calculation of matrices by Cramer's method. Cramer's method for solving systems of linear equations. Matrix Actions

Consider a system of 3 equations with three unknowns

Using third-order determinants, the solution of such a system can be written in the same form as for a system of two equations, i.e.

(2.4)

if 0. Here

It is Cramer's rule solving a system of three linear equations in three unknowns.

Example 2.3. Solve a system of linear equations using Cramer's rule:

Solution . Finding the determinant of the main matrix of the system

Since 0, then to find a solution to the system, you can apply Cramer's rule, but first calculate three more determinants:

Examination:

Therefore, the solution is found correctly. 

Cramer's rules obtained for linear systems of the 2nd and 3rd order suggest that the same rules can be formulated for linear systems of any order. Really takes place

Cramer's theorem. Quadratic system of linear equations with a non-zero determinant of the main matrix of the system (0) has one and only one solution, and this solution is calculated by the formulas

(2.5)

Where  – main matrix determinant,  i – matrix determinant, derived from the main, replacementith column free members column.

Note that if =0, then Cramer's rule is not applicable. This means that the system either has no solutions at all, or has infinitely many solutions.

Having formulated Cramer's theorem, the question naturally arises of calculating higher-order determinants.

2.4. nth order determinants

Additional minor M ij element a ij is called the determinant obtained from the given by deleting i-th line and j-th column. Algebraic addition A ij element a ij is called the minor of this element, taken with the sign (–1) i + j, i.e. A ij = (–1) i + j M ij .

For example, let's find minors and algebraic complements of elements a 23 and a 31 determinants

We get



Using the concept of algebraic complement, we can formulate the determinant expansion theoremn-th order by row or column.

Theorem 2.1. Matrix determinantAis equal to the sum of the products of all elements of some row (or column) and their algebraic complements:

(2.6)

This theorem underlies one of the main methods for calculating determinants, the so-called. order reduction method. As a result of the expansion of the determinant n th order in any row or column, we get n determinants ( n–1)-th order. In order to have fewer such determinants, it is advisable to choose the row or column that has the most zeros. In practice, the expansion formula for the determinant is usually written as:

those. algebraic additions are written explicitly in terms of minors.

Examples 2.4. Calculate the determinants by first expanding them in any row or column. Usually in such cases, choose the column or row that has the most zeros. The selected row or column will be marked with an arrow.



2.5. Basic properties of determinants

Expanding the determinant in any row or column, we get n determinants ( n–1)-th order. Then each of these determinants ( n–1)-th order can also be decomposed into a sum of determinants ( n–2)th order. Continuing this process, one can reach the determinants of the 1st order, i.e. to the elements of the matrix whose determinant is being calculated. So, to calculate the 2nd order determinants, you will have to calculate the sum of two terms, for the 3rd order determinants - the sum of 6 terms, for the 4th order determinants - 24 terms. The number of terms will increase sharply as the order of the determinant increases. This means that the calculation of determinants of very high orders becomes a rather laborious task, beyond the power of even a computer. However, determinants can be calculated in another way, using the properties of determinants.

Property 1 . The determinant will not change if rows and columns are swapped in it, i.e. when transposing a matrix:

This property indicates the equality of rows and columns of the determinant. In other words, any statement about the columns of a determinant is true for its rows, and vice versa.

Property 2 . The determinant changes sign when two rows (columns) are interchanged.

Consequence . If the determinant has two identical rows (columns), then it is equal to zero.

Property 3 . The common factor of all elements in any row (column) can be taken out of the sign of the determinant.

For example,

Consequence . If all elements of some row (column) of the determinant are equal to zero, then the determinant itself is equal to zero.

Property 4 . The determinant will not change if the elements of one row (column) are added to the elements of another row (column) multiplied by some number.

For example,

Property 5 . The determinant of the matrix product is equal to the product of the matrix determinants:

Cramer's method is based on the use of determinants in solving systems of linear equations. This greatly speeds up the solution process.

Cramer's method can be used to solve a system of as many linear equations as there are unknowns in each equation. If the determinant of the system is not equal to zero, then Cramer's method can be used in the solution; if it is equal to zero, then it cannot. In addition, Cramer's method can be used to solve systems of linear equations that have a unique solution.

Definition. The determinant, composed of the coefficients of the unknowns, is called the determinant of the system and is denoted by (delta).

Determinants

are obtained by replacing the coefficients at the corresponding unknowns by free terms:

;

Cramer's theorem. If the determinant of the system is nonzero, then the system of linear equations has one single solution, and the unknown is equal to the ratio of the determinants. The denominator is the determinant of the system, and the numerator is the determinant obtained from the determinant of the system by replacing the coefficients with the unknown by free terms. This theorem holds for a system of linear equations of any order.

Example 1 Solve the system of linear equations:

According to Cramer's theorem we have:

So, the solution of system (2):

online calculator, Cramer's solution method.

Three cases in solving systems of linear equations

As appears from Cramer's theorems, when solving a system of linear equations, three cases may occur:

First case: the system of linear equations has a unique solution

(the system is consistent and definite)

Second case: the system of linear equations has an infinite number of solutions

(the system is consistent and indeterminate)

** ,

those. the coefficients of the unknowns and the free terms are proportional.

Third case: the system of linear equations has no solutions

(system inconsistent)

So the system m linear equations with n variables is called incompatible if it has no solutions, and joint if it has at least one solution. A joint system of equations that has only one solution is called certain, and more than one uncertain.

Examples of solving systems of linear equations by the Cramer method

Let the system

Based on Cramer's theorem

………….
,

Where
-

system identifier. The remaining determinants are obtained by replacing the column with the coefficients of the corresponding variable (unknown) with free members:

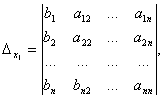
Example 2

Therefore, the system is definite. To find its solution, we calculate the determinants

By Cramer's formulas we find:

So, (1; 0; -1) is the only solution to the system.

To check the solutions of systems of equations 3 X 3 and 4 X 4, you can use the online calculator, the Cramer solving method.

If there are no variables in the system of linear equations in one or more equations, then in the determinant the elements corresponding to them are equal to zero! This is the next example.

Example 3 Solve the system of linear equations by Cramer's method:

Solution. We find the determinant of the system:

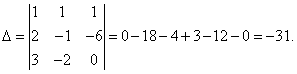
Look carefully at the system of equations and at the determinant of the system and repeat the answer to the question in which cases one or more elements of the determinant are equal to zero. So, the determinant is not equal to zero, therefore, the system is definite. To find its solution, we calculate the determinants for the unknowns

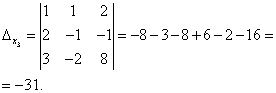
By Cramer's formulas we find:

So, the solution of the system is (2; -1; 1).

To check the solutions of systems of equations 3 X 3 and 4 X 4, you can use the online calculator, the Cramer solving method.

Top of page

We continue to solve systems using the Cramer method together

As already mentioned, if the determinant of the system is equal to zero, and the determinants for the unknowns are not equal to zero, the system is inconsistent, that is, it has no solutions. Let's illustrate with the following example.

Example 6 Solve the system of linear equations by Cramer's method:

Solution. We find the determinant of the system:

The determinant of the system is equal to zero, therefore, the system of linear equations is either inconsistent and definite, or inconsistent, that is, it has no solutions. To clarify, we calculate the determinants for the unknowns

The determinants for the unknowns are not equal to zero, therefore, the system is inconsistent, that is, it has no solutions.

To check the solutions of systems of equations 3 X 3 and 4 X 4, you can use the online calculator, the Cramer solving method.

In problems on systems of linear equations, there are also those where, in addition to the letters denoting variables, there are also other letters. These letters stand for some number, most often a real number. In practice, such equations and systems of equations lead to problems to find the general properties of any phenomena and objects. That is, you invented some new material or device, and to describe its properties, which are common regardless of the size or number of copies, you need to solve a system of linear equations, where instead of some coefficients for variables there are letters. You don't have to look far for examples.

The next example is for a similar problem, only the number of equations, variables, and letters denoting some real number increases.

Example 8 Solve the system of linear equations by Cramer's method:

Solution. We find the determinant of the system:

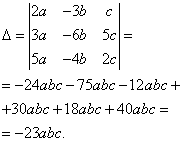
Finding determinants for unknowns

In order to master this paragraph, you must be able to open the qualifiers "two by two" and "three by three". If qualifiers are bad, please study the lesson How to calculate the determinant?

We first consider Cramer's rule in detail for a system of two linear equations in two unknowns. For what? “After all, the simplest system can be solved by the school method, by term-by-term addition!

The fact is that even if sometimes, but there is such a task - to solve a system of two linear equations with two unknowns using Cramer's formulas. Secondly, a simpler example will help you understand how to use Cramer's rule for a more complex case - a system of three equations with three unknowns.

In addition, there are systems of linear equations with two variables, which it is advisable to solve exactly according to Cramer's rule!

Consider the system of equations

At the first step, we calculate the determinant , it is called the main determinant of the system.

Gauss method.

If , then the system has a unique solution, and to find the roots, we must calculate two more determinants:
And

In practice, the above qualifiers can also be denoted by the Latin letter.

The roots of the equation are found by the formulas:
,

Example 7

Solve a system of linear equations

Solution: We see that the coefficients of the equation are quite large, on the right side there are decimal fractions with a comma. The comma is a rather rare guest in practical tasks in mathematics; I took this system from an econometric problem.

How to solve such a system? You can try to express one variable in terms of another, but in this case you will surely get terrible fancy fractions, which are extremely inconvenient to work with, and the design of the solution will look just awful. You can multiply the second equation by 6 and subtract term by term, but the same fractions will appear here.

What to do? In such cases, Cramer's formulas come to the rescue.

;

Answer: ,

Both roots have infinite tails and are found approximately, which is quite acceptable (and even commonplace) for econometrics problems.

Comments are not needed here, since the task is solved according to ready-made formulas, however, there is one caveat. When using this method, compulsory The fragment of the assignment is the following fragment: "so the system has a unique solution". Otherwise, the reviewer may punish you for disrespecting Cramer's theorem.

It will not be superfluous to check, which is convenient to carry out on a calculator: we substitute the approximate values \u200b\u200bin the left side of each equation of the system. As a result, with a small error, numbers that are on the right side should be obtained.

Example 8

Express your answer in ordinary improper fractions. Make a check.

This is an example for an independent solution (example of fine design and answer at the end of the lesson).

We turn to the consideration of Cramer's rule for a system of three equations with three unknowns:

We find the main determinant of the system:

If , then the system has infinitely many solutions or is inconsistent (has no solutions). In this case, Cramer's rule will not help, you need to use the Gauss method.

If , then the system has a unique solution, and to find the roots, we must calculate three more determinants:
, ,

And finally, the answer is calculated by the formulas:

As you can see, the “three by three” case is fundamentally no different from the “two by two” case, the column of free terms sequentially “walks” from left to right along the columns of the main determinant.

Example 9

Solve the system using Cramer's formulas.

Solution: Let's solve the system using Cramer's formulas.

, so the system has a unique solution.

Answer: .

Actually, there is nothing special to comment here again, in view of the fact that the decision is made according to ready-made formulas. But there are a couple of notes.

It happens that as a result of calculations, “bad” irreducible fractions are obtained, for example: .
I recommend the following "treatment" algorithm. If there is no computer at hand, we do this:

1) There may be a mistake in the calculations. As soon as you encounter a “bad” shot, you must immediately check whether is the condition rewritten correctly. If the condition is rewritten without errors, then you need to recalculate the determinants using the expansion in another row (column).

2) If no errors were found as a result of the check, then most likely a typo was made in the condition of the assignment. In this case, calmly and CAREFULLY solve the task to the end, and then make sure to check and draw it up on a clean copy after the decision. Of course, checking a fractional answer is an unpleasant task, but it will be a disarming argument for the teacher, who, well, really likes to put a minus for any bad thing like. How to deal with fractions is detailed in the answer for Example 8.

If you have a computer at hand, then use an automated program to check it, which can be downloaded for free at the very beginning of the lesson. By the way, it is most advantageous to use the program right away (even before starting the solution), you will immediately see the intermediate step at which you made a mistake! The same calculator automatically calculates the solution of the system using the matrix method.

Second remark. From time to time there are systems in the equations of which some variables are missing, for example:

Here in the first equation there is no variable , in the second there is no variable . In such cases, it is very important to correctly and CAREFULLY write down the main determinant:
– zeros are put in place of missing variables.
By the way, it is rational to open determinants with zeros in the row (column) in which zero is located, since there are noticeably fewer calculations.

Example 10

Solve the system using Cramer's formulas.

This is an example for self-solving (finishing sample and answer at the end of the lesson).

For the case of a system of 4 equations with 4 unknowns, Cramer's formulas are written according to similar principles. You can see a live example in the Determinant Properties lesson. Reducing the order of the determinant - five 4th order determinants are quite solvable. Although the task is already very reminiscent of a professor's shoe on the chest of a lucky student.

Solution of the system using the inverse matrix

The inverse matrix method is essentially a special case matrix equation(See Example No. 3 of the specified lesson).

To study this section, you need to be able to expand the determinants, find the inverse matrix and perform matrix multiplication. Relevant links will be given as the explanation progresses.

Example 11

Solve the system with the matrix method

Solution: We write the system in matrix form:
, Where

Please look at the system of equations and the matrices. By what principle we write elements into matrices, I think everyone understands. The only comment: if some variables were missing in the equations, then zeros would have to be put in the corresponding places in the matrix.

We find the inverse matrix by the formula:
, where is the transposed matrix of algebraic complements of the corresponding elements of the matrix .

First, let's deal with the determinant:

Here the determinant is expanded by the first line.

Attention! If , then the inverse matrix does not exist, and it is impossible to solve the system by the matrix method. In this case, the system is solved by the elimination of unknowns (Gauss method).

Now you need to calculate 9 minors and write them into the matrix of minors

Reference: It is useful to know the meaning of double subscripts in linear algebra. The first digit is the line number in which the element is located. The second digit is the number of the column in which the element is located:

That is, a double subscript indicates that the element is in the first row, third column, while, for example, the element is in the 3rd row, 2nd column

In the course of solving, it is better to describe the calculation of minors in detail, although, with a certain experience, they can be adjusted to count with errors orally.

In the first part, we considered some theoretical material, the substitution method, as well as the method of term-by-term addition of system equations. To everyone who came to the site through this page, I recommend that you read the first part. Perhaps some visitors will find the material too simple, but in the course of solving systems of linear equations, I made a number of very important remarks and conclusions regarding the solution of mathematical problems in general.

And now we will analyze Cramer's rule, as well as the solution of a system of linear equations using the inverse matrix (matrix method). All materials are presented simply, in detail and clearly, almost all readers will be able to learn how to solve systems using the above methods.

In addition, there are systems of linear equations with two variables, which it is advisable to solve exactly according to Cramer's rule!

Consider the system of equations

At the first step, we calculate the determinant , it is called the main determinant of the system.

Gauss method.

If , then the system has a unique solution, and to find the roots, we must calculate two more determinants:
And

In practice, the above qualifiers can also be denoted by the Latin letter.

The roots of the equation are found by the formulas:
,

Example 7

Solve a system of linear equations

What to do? In such cases, Cramer's formulas come to the rescue.

;

Answer: ,

Both roots have infinite tails and are found approximately, which is quite acceptable (and even commonplace) for econometrics problems.

Example 8

Express your answer in ordinary improper fractions. Make a check.

This is an example for an independent solution (example of fine design and answer at the end of the lesson).

We turn to the consideration of Cramer's rule for a system of three equations with three unknowns:

We find the main determinant of the system:

If , then the system has infinitely many solutions or is inconsistent (has no solutions). In this case, Cramer's rule will not help, you need to use the Gauss method.

If , then the system has a unique solution, and to find the roots, we must calculate three more determinants:
, ,

And finally, the answer is calculated by the formulas:

Example 9

Solve the system using Cramer's formulas.

Solution: Let's solve the system using Cramer's formulas.

, so the system has a unique solution.

Answer: .

Actually, there is nothing special to comment here again, in view of the fact that the decision is made according to ready-made formulas. But there are a couple of notes.

It happens that as a result of calculations, “bad” irreducible fractions are obtained, for example: .
I recommend the following "treatment" algorithm. If there is no computer at hand, we do this:

Second remark. From time to time there are systems in the equations of which some variables are missing, for example:

Here in the first equation there is no variable , in the second there is no variable . In such cases, it is very important to correctly and CAREFULLY write down the main determinant:
– zeros are put in place of missing variables.
By the way, it is rational to open determinants with zeros according to the row (column) in which zero is located, since there are noticeably fewer calculations.

Example 10

Solve the system using Cramer's formulas.

This is an example for self-solving (finishing sample and answer at the end of the lesson).

Solution of the system using the inverse matrix

The inverse matrix method is essentially a special case matrix equation(See Example No. 3 of the specified lesson).

To study this section, you need to be able to expand the determinants, find the inverse matrix and perform matrix multiplication. Relevant links will be given as the explanation progresses.

Example 11

Solve the system with the matrix method

Solution: We write the system in matrix form:
, Where

We find the inverse matrix by the formula:
, where is the transposed matrix of algebraic complements of the corresponding elements of the matrix .

First, let's deal with the determinant:

Here the determinant is expanded by the first line.

Now you need to calculate 9 minors and write them into the matrix of minors

Methods Kramer And Gaussian one of the most popular solutions SLAU. In addition, in some cases it is advisable to use specific methods. The session is close, and now is the time to repeat or master them from scratch. Today we deal with the solution by the Cramer method. After all, solving a system of linear equations by Cramer's method is a very useful skill.

Systems of linear algebraic equations

The system of linear algebraic equations is a system of equations of the form:

Value set x , at which the equations of the system turn into identities, is called the solution of the system, a And b are real coefficients. A simple system consisting of two equations with two unknowns can be solved mentally or by expressing one variable in terms of the other. But there can be much more than two variables (x) in SLAE, and simple school manipulations are indispensable here. What to do? For example, solve SLAE by Cramer's method!

So let the system be n equations with n unknown.

Such a system can be rewritten in matrix form

Here A is the main matrix of the system, X And B , respectively, column matrices of unknown variables and free members.

SLAE solution by Cramer's method

If the determinant of the main matrix is not equal to zero (the matrix is nonsingular), the system can be solved using the Cramer method.

According to the Cramer method, the solution is found by the formulas:

Here delta is the determinant of the main matrix, and delta x n-th - the determinant obtained from the determinant of the main matrix by replacing the n-th column with a column of free terms.

This is the whole point of Cramer's method. Substituting the values found by the above formulas x into the desired system, we are convinced of the correctness (or vice versa) of our solution. To help you quickly grasp the essence, we give below an example of a detailed solution of SLAE by the Cramer method:

Even if you don't succeed the first time, don't be discouraged! With a little practice, you'll start popping SLOWs like nuts. Moreover, now it is absolutely not necessary to pore over a notebook, solving cumbersome calculations and writing on the rod. It is easy to solve SLAE by the Cramer method online, just by substituting the coefficients into the finished form. You can try the online calculator for solving the Cramer method, for example, on this site.

And if the system turned out to be stubborn and does not give up, you can always ask our authors for help, for example, to buy a synopsis. If there are at least 100 unknowns in the system, we will definitely solve it correctly and just in time!